Proporcionalidad directa
Para recordar:
|
Dos cantidades son directamente proporcionales cuando aumentan o
disminuyen en la misma proporción. Ej.: Si duplico la cantidad de alfajores, duplico la cantidad de dulce. Si tengo la mitad de un alfajor ½ voy a necesitar la mitad de dulce
1/8 . La constante de
proporcionalidad es el valor que le corresponde a una unidad. En este
caso es ¼. |
Resolver los ejercicios 9 y 10 de
la pág. 138.
Completar los ejercicios de las páginas 135 y 136.
SEGUIMOS CON
FRACCIONES
Resolver los ejercicios de las páginas 118, 119 y 120.
Recta numérica
1)
Se sabe que este triángulo representa
La respuesta de Marcela fue:
La respuesta de Martín fue:
¿Quién de los dos resolvió correctamente el problema?
2)
¿En cuáles de los siguientes dibujos se pintó la
cuarta parte?
Explicá cómo lo pensaste en cada caso.
3) ¿Cuáles
de las siguientes fracciones son mayores que un entero? Explicá cómo lo
pensaste.
4) ¿Cuánto
le falta a cada una de estas fracciones para llegar a 1?
5) ¿Cuánto
le falta a cada una de estas fracciones para llegar a 2?
¡Más Fracciones!
Resolvemos:
1-
Javier se sirvió dos porciones del postre
helado; Lionel, el doble que Javier, y Diego, una menos que Lionel.
|
|
|
|
|
|
|
|
|
|
|
|
|
a) ¿Cuál de estos cálculos muestran la fracción del postre que comieron los tres? Rodealos
b)
¿Qué fracción del postre comieron entre todos?
c)
¿Con qué
cálculo podés mostrar qué fracción del postre sobró?
2-
El lunes pinté un tercio de la pared y el
martes, la sexta parte.
a-
¿Qué fracción de la pared pinté? ____
b-
¿Qué fracción me falta pintar? ____
|
|
|
|
|
|
|
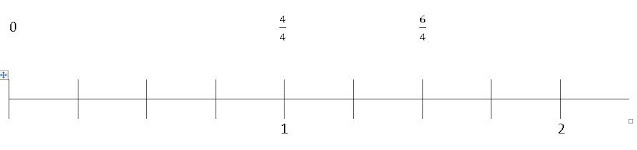
3- Ubicar fracciones en las siguiente recta numérica.
![]()
![]()
![]()
![]()
![]()

PROBLEMAS PARA SEGUIR REPARTIENDO.
RESOLVER
1- Matías
tiene 3 chocolates para repartir entre 5 chicos. ¿Son equivalentes las
siguientes formas de reparto?:
a) Parte
cada chocolate en 5 partes iguales y le da una parte de cada chocolate a cada
chico;
b) Parte
por la mitad cada uno de los 3 chocolates y da una mitad a cada chico, y parte
en 5 la última mitad.
Expresá en fracciones los resultados de ambos repartos.
2- Encontrá tres formas equivalentes de repartir 8
chocolates entre 3 chicos.
Completar las páginas 84, 85 y 86.
GEOMETRÍA
Completar la página 99.
(Trabajaremos estos temas en el zoom)
COMPLETAR LOS EJERCICIOS DE LA PÁG 82 Y 83.
GEOMETRÍA
1-
Dibujar un ángulo de 90° otro de 165° y otro de
45° (en distintas direcciones).
2-
Clasificarlos según su abertura.
3-
Completamos la página 97 y 98 del libro.
(lo trabajaremos en zoom)
1-Completar la página 81
|
Para
recordar: Si
se divide un entero en dos partes iguales, cada una de esas partes se llama
_______________ y se escribe_____ Si
se juntan dos pedacitos de ½ se forma un_________ Si
se divide un entero en cuatro partes iguales, cada una de esas partes se
llama ____________ y se escribe______ Si
se juntan cuatro pedacitos de ¼ se
forma un_________ |
Responder:
a - Si tengo ¼ ¿cuál sería la fracción para
completar el entero?
b- Si tengo
2/3 ¿cuál sería la fracción para completar el entero?
c- Si tengo 3/6 ¿cuál sería la fracción para
completar el entero?
d- Si tengo 3/8 ¿cuál sería la fracción para
completar el entero?
e- Laura comió 1/2 chocolate y Mario 2/4
chocolate, ¿quién comió más?
LAS FRACCIONES
Completar las páginas 79 y 80 del libro de Matemática.
Problemas para seguir repartiendo.
1)
¿Cómo podría hacerse el reparto si ahora fuesen
27 los chocolates y 4 lo niños?
2)
¿Y si los niños siguieran siendo 4 y sólo
hubiera 6 chocolates?
3)
¿Y si los chocolates fueran 23 y los chicos 5?
¿Cómo podrían repartirse?
PROBLEMAS PARA SEGUIR REPARTIENDO
1)
Se desea repartir 17 chocolates entre 4 niños,
de modo tal que cada uno reciba la misma cantidad y todo el chocolate sea
repartido, ¿Cómo puede efectuarse el
reparto?
2)
De manera similar que en el problema anterior:
a)
Repartir 21 chocolates entre 5 niños.
b)
Repartir 10 chocolates entre 3 niños.
c)
Repartir 1 chocolate entre 8 niños.
d)
Repartir 25 chocolates entre 4 niños.
Utilizá cualquier manera para repartir. (Se
puede dibujar)
Resolvemos solitos/as y con todo lo que ya hemos visto.
1- Se
reparten 10 chocolates entre 3 niños; todos reciben la misma cantidad. ¿Cuántos
chocolates le tocan a cada uno?
2- Se
reparten 17 autitos entre 4 niños; todos
reciben la misma cantidad. ¿Cuántos autitos le tocan a cada uno?
3- Cuatro amigos deciden repartir, entre ellos y en partes iguales, $ 21 que obtuvieron en un premio de lotería. ¿Cuánto le corresponde a cada uno?
4- Con
una cinta de papel de 46 cm se arman 4 escarapelas iguales. ¿Qué largo tiene
cada escarapela?
Seguramente habrás comprobado que ninguno
de los repartos anteriores “da justo”, en todos sobra.
En algunos casos, lo que sobra se puede
seguir repartiendo, y en otros, no. Analizá los cuatro problemas que resolviste
y establecé en qué casos el resto obtenido se puede seguir repartiendo.
ESTAS SITUACIONES PROBLEMÁTICAS SE TRABAJARÁN EN EL ZOOM.
¡A pensar!
1. Para equipar uno de sus salones, la administración de un centro cultural encargó 560 sillas iguales y 38 sillones. En total, se pagaron $ 42.062
Si cada silla costó $65, ¿cuánto costó cada sillón?
2. En un teatro, hay 45 filas con 19 asientos en cada una de ellas. ¿Cuántas filas con la misma cantidad de asientos en cada una habría que agregar para tener, en total, 1900 asientos? Resolvé el problema de dos maneras diferentes.
3. Resolver las actividades de la página 96.
4.

Producto a envasar en cajas de 10
unidades.
|
Cantidad de cajas de 10 unidades
|
Producto a envasar en cajas de 100
unidades.
|
Cantidad de cajas de 100 unidades
|
789 tornillos
|
937 remaches
|
||
908 tuercas
|
2133 arandelas
|
||
2145 clavos
|
1098 bulones
|
||
1- Todos los días Marisa gasta $ 6 en el colectivo y en alguna golosina. Si tiene $ 98, ¿para cuántos días le alcanza?

Actividades del 13/07 al 17/07
Realizá las actividades propuestas en la página 42 del libro.
Actividades del 29/06 al 03/07
En el cálculo de la división hay una
parte que llamamos resto.
A veces cuando dividimos un número por
otro puede sobrar una cantidad. Esa cantidad sobra pues no alcanza para seguir repartiendo en partes
iguales o para seguir armando grupos de la misma
cantidad de elementos.
Eso pasa cuando el número que vamos a
dividir no está en la tabla.
Cuando el número que vamos a dividir
sí está en la tabla, el resto es igual
a 0, o sea no sobra ninguna cantidad.
Cuando el número a dividir no está en la tabla, la división va a
tener un resto que no es cero. Puede ser 1, 2, 3, 4, etc., todo
depende de por cuál número estoy dividiendo
Por ejemplo:
|
¿SOBRA?
SI / NO
|
¿POR
QUÉ?
|
|
46 : 5
|
||
27 : 9
|
||
40 : 8
|
||
42 : 8
|
||
44 : 8
|
Al dividir aunque no encontremos el
número que buscamos en la tabla, de todos modos, podemos usarla y nos puede
ayudar a hacer el cálculo.
Por ejemplo: Para dividir 23 chupetines entre 5
nenes, miramos en la tabla del 5 y podemos usar el 20, o sea puedo usar 20
chupetines, que es el número que más cerca está del 23 pero sin pasarse (no
puedo pasarme,¡¡no tengo más que 23 chupetines!!). Como5 x4= 20,
entonces puedo darle 4 a cada nene y sobran 3 chupetines, pues 23 – 20 = 3.
|
...... : 2 =
|
...... : 5 =
|
…..: 8 =
|
…..: 10 =
|
..... : 2 =
|
..... : 6 =
|
..... : 5 =
|
..... : 3 =
|
.. : 9 =
|
Actividades del 16/6 al 19/6
CANTIDAD DE CARAMELOS
|
PAQUETES DE A 6 CARAMELOS
|
¿SOBRAN CARAMELOS? ¿CUÁNTOS?
|
14
|
||
18
|
||
19
|
||
24
|
||
26
|
||
31
|
x
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
1
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
2
|
2
|
4
|
6
|
8
|
10
|
12
|
14
|
16
|
18
|
20
|
3
|
3
|
6
|
9
|
12
|
15
|
18
|
21
|
24
|
27
|
30
|
4
|
4
|
8
|
12
|
16
|
20
|
24
|
28
|
32
|
36
|
40
|
5
|
5
|
10
|
15
|
20
|
25
|
30
|
35
|
40
|
45
|
50
|
6
|
6
|
12
|
18
|
24
|
30
|
36
|
42
|
48
|
54
|
60
|
7
|
7
|
14
|
21
|
28
|
35
|
42
|
49
|
56
|
63
|
70
|
8
|
8
|
16
|
24
|
32
|
40
|
48
|
56
|
64
|
72
|
80
|
9
|
9
|
18
|
27
|
36
|
45
|
54
|
63
|
72
|
81
|
90
|
10
|
10
|
20
|
30
|
40
|
50
|
60
|
70
|
80
|
90
|
100
|
2. Usando la tabla, escribí el resultado de las siguientes divisiones y escribí qué cálculo usaste para resolverlas. El primero ya está resuelto y va como ejemplo.
X
|

































No hay comentarios:
Publicar un comentario